TRADICIÓN BELENÍSTICA SEVILLANA

En la  llegada de la Navidad en Sevilla destaca la aparición de belenes por todo el centro de la capital. Un grupo de nosotros estuvimos visitando algunos, los que pudimos en una mañana. Resulta muy gratificante su contemplación, para los niños es como un mundo de fantasía, fuera de lo cotidiano a lo que están acostumbrados, un viaje a un pasado lleno de ilusión. Pero los mayores también lo disfrutamos, por una parte pensando en la felicidad de los pequeños y por otra por el propio placer que produce  contemplar estas obras de arte en que se constituyen los belenes; para mi mirarlos es como si te acogiera tu ciudad, tu tierra y el mundo entero. Si, verlos y decir Navidad es lo mismo.

Estuvimos viendo el de la calle Imagen, que no es muy grande pero acogedor. Se ven dos partes, lo que atañe al mismo Belén con la sagrada familia y los animales de labor y por ejemplo la adoración de los pastores y luego como por otra parte el viaje de los magos por el oriente, con figuras de Egipto muy bien esculpidas. Me digo a mi mismo al recordarlo lo bonito que es un belén y el arte que hay que tener para hacerlos. Estuvimos también en el del Diario de Sevilla, mas pequeño que el anterior, se encuentra a la entrada misma de este diario, y las figuras y el montaje son un poco mas escasos, pero muy bonitos también, eso si parece dispuesto con un poco de menos mimo que el otro, aunque no se decir si solo es que es mas austero, con figuras como más rígidas o en posiciones mas forzadas que en el otro belén. Paseamos un poco más por el centro y quisimos visitar el que tenían en el Círculo Mercantil. Aquí, según sé, han hecho un belén de chocolate y miel. No pudimos entrar. Eran eso de las doce y había una gran cola de padres y muchos niños. Los niños disfrutarían como nadie con la particularidad de este belén. Nos quedamos con las ganas de ver este particular belén.

Finalmente visitamos el belén de la Fundación Cajasol, el mas grande de ellos. Este belén tiene por motivo central la Epifanía del Señor, lo que le ha dado nombre, compuesto por esculturas y estructuras de Luís Garduño. Consta de 100 figuras de candelero de 40 centímetros, acompañadas de una gran variedad de complementos y pequeños detalles. Las construcciones están realizadas con poliexpan, con adornos en madera y telas. El belén recrea siete escenas: La Anunciación, donde el ángel Gabriel, enviado por Dios a la ciudad de Galilea, visita a la Virgen María; Negación de posada, en la que María permanece junto al asno mientras José busca cobijo ante el alumbramiento; El mercado, que recrea el zoco de Nazaret. La anunciación del ángel a los pastores. Ya ha nacido el Salvador y unos pastores que pasan la noche velando al rebaño reciben la visita de un al ángel que les anuncia: “la gloria de Dios os envolverá con su claridad”. La Cabalgata de los Reyes Magos, donde tres sabios del Lejano Oriente deciden seguir la estela de una estrella, que les conduce a un gran acontecimiento, El Nacimiento de Jesús. 

Los Reyes magos llegan al lugar donde está el niño con María para ofrecerle oro, incienso y mirra, reconociendo la naturaleza mesiánica de Cristo, su divinidad y su humanidad. Por último el empadronamiento, donde María y José, recién llegados a las puertas de Belén, inscriben al Mesías recién nacido. Si venís por Sevilla no dejéis de visitar algún belén.

Jesús Ocaña.

MIENTRAS OS RECUERDE...

He tenido siempre, desde que murieron mis padres, una cosa en la cabeza. Mientras te recuerde alguien que está vivo, sigues vivo y nunca morirás. No sé si lo he escuchado en algún sitio o lo he leído en algún libro pero tengo en mi interior esa convicción.  Creo que, entre otras cosas, por esto cada día me acuerdo de ellos y, además, tengo sueños constantes donde aparecen sus figuras, a veces de forma enigmática , otras queriendo decirme algo, cosas que a veces creo entender y en otros momentos, sucesos que escapan a mi interpretación, porque aunque no creo que los sueños nos revelan el futuro , si creo que tienen algo que ver con lo que nos está pasando en el momento y por eso se pueden  explicar de una forma coherente, aunque haya veces que parezcan no tener ningún significado.

Pienso que cuando mueres todo acaba, que ya no hay nada más detrás de la muerte y que  no existe una vida del mas allá ni otra forma de existencia. Por eso me gusta creer en lo que he dicho antes, en lo de recordar a los seres queridos personas que aun siguen vivas. Mi padre o mi madre no hicieron nada que quedara grabado en los anales de la historia como si lo han hecho otras personajes que han pasado a la posteridad. Ellos vivirán mientras yo los recuerde y tengo presente que esto será mientras viva. Ahora no tengo hijos ni ninguna carga familiar, quizás por eso pienso así.

Duermo tranquilo. No me asusto de tenerlos siempre en la memoria y tampoco me da ninguna extraña sensación cuando despierto por el hecho de haber soñado con ellos. Es más, cuando pasa algún tiempo y ellos no aparecen en mis sueños, me siento solo. Desde que murieron mis padres la relación con mis hermanas es cada vez menor. Ni siquiera nos llamamos una vez al mes ni nada por el estilo. Cuando a alguno de nosotros le entra remordimientos entonces nos acordamos de los hermanos y nos llamamos. Para eso pueden pasar meses. Como siete u ocho. Entonces el hecho de que yo sueñe con mis padres me hace sentir aquella época en que éramos una familia. Soy gilipollas  por pensar esto, pero es lo único que me queda.

No creo en el más allá, ni en ninguna otra forma de vida por eso me parece tan importante la huella que haya dejado una persona sobre otra y como actúa esta sobre ella. Nos morimos y se acabo todo. No soy católico, ni budista, ni me convence la doctrina de ninguna religión. Creo que debe de haber algo que haya creado todo esto, llamémosle Dios, pero no creo que tengamos que redimirnos de nuestros pecados por que no es esa la idea que me trasmite la Naturaleza y mi capacidad de observación. Creo en la ética y en la moral, en los Principios, y en todo lo que sea la conservación de la vida. Creo en los derechos y  además creo que los modelos de gobierno menos malo  es la democracia, pero no creo en un  dios como han intentado venderme desde que era pequeño. Siempre dudé.

No quiero que este texto sea una declaración de mis convicciones y tampoco desarrollar un ensayo sobre la vida y la muerte. Todo esto lo he escrito porque quería decir una cosa. A pesar de que han pasado diez años y lo he pasado muy mal en la vida (he llegado a vivir en la calle) recuerdo el amor que me trasmitía mi madre y el cariño que empleaba mi padre al hablarme. He perdido a toda mi familia. Tan solo tengo contacto con una prima y una hermana de forma esporádica. Más con mi prima que con mi hermana y, la verdad, cuando la he necesitado la he tenido junto a mí, a pesar de tener ella su vida y su familia. Pero lo que no puedo olvidar ni perdonar, por mucho que lo intento removiendo mi conciencia e intentando comprender todo lo que sucedió para que yo acabara en la calle, es que mi familia me dejara solo y como consecuencia, vivir en la calle.

Hoy es 20 de diciembre y hace casi tres meses que no tomo alcohol ni drogas. Que mejor manera de celebrarlo que recordando a mis padres. He tenido mucha ayuda pero de nada ha servido hasta hace unos meses. No comprendía que yo era un alcohólico por mucho y de muchas formas que me lo explicaran. Pero hoy no es un día para mirar al pasado sino al futuro, e intentar conseguir el objetivo final. Tener una vida normalizada.

Pedro Sánchez 

EL POEMA DEL FIN DEL MUNDO

NUBE "V"

Detrás del espiral

se ve la nube "V"

detrás de la nube "V"

se ve el espiral.

Es la esfera de nuestra alma,

es la esfera universal.

Dentro de la esfera,

se escucha una voz.

Dimensión, via astral,

dimensión.

Uh, uh,uh,uh,uh

uh, uh,

Flota como el aire

explota como el viento,

como lagartija con el sol adentro.

Nube "V", nube "V".

Francisco Manuel Ortiz Guisado

ESTIMULA TU MENTE NAVIDEÑO

Ejercicios de estimulación cognitiva. ¿Quién se repite mas veces?

Solución ejercicios anteriores.

                                                   

TABAQUISMO

El tabaquismo para mi se ha convertido en un verdadero problema. En las últimas semanas me he encontrado en una encrucijada: el tabaco o mi salud. Entre la espada y la pared.

 Empecé con la tontería de querer parecer mayor a la edad de 16 años. Eso te lo inculcaba la sociedad, el mundo que te rodeaba. Un grupo de tres amigos que nos reuníamos todos los fines de semana, decidimos un día comprarnos un paquete de cigarrillos para todos, y hacíamos como que fumábamos, pero no nos tragábamos el humo. Así estuvimos un año. Al principio fumábamos a escondidas, y yo me sentía mal por fumar sin que lo supieran mis padres. Cuando llegué a Sevilla, a la edad de 17 años, en los recreos del instituto, haciendo COU, me fumaba algún cigarrillo. Algunas amigas me veían fumar pero no tragarme el humo, pues era para mí y para los amigos de mi pueblo como un juego para parecer más adultos. Entonces muchos adultos fumaban. En mi familia y en la de mis amigos, los mayores no fumaban. Una de estas amigas, como digo en un recreo, me dijo que el humo había que tirárselo a pecho, cosa que hacían todos ellos, así que desde ese momento empecé a fumar en el sentido más exacto de la palabra, “tirándome” el tabaco a pecho.

Decidí fumar y le pedí permiso a mi padre, al que no le hizo mucha gracia, pero me dijo que bueno, creo que esperando que lo dejara pronto. En un año, mi primer año en Sevilla, como digo con 17 años, terminé por fumarme un paquete diario. En la casa que vivía, compartiendo piso con un compañero que estaba estudiando magisterio, ya me llamaban la atención por fumar. Su madre me decía siempre: ¡ no fumes tanto no ves como se están poniendo las paredes de amarillas!. Pasé a fumar en la ventana, pero seguí fumando, no podía dejarlo ya entonces. Fumé mientras estudiaba en la facultad, pues en aquel tiempo se podía fumar incluso dentro del aula, mientras el profesor impartía clase. Esto lo hacía yo pocas veces, pero lo hacía de vez en cuando. Con unos 24 años intenté dejar de fumar y estuve seis meses. Después de la época de estudios y del servicio militar llegó la hora de trabajar; fue la época en que se produjo la ruptura con la novia que tenía. Se acumularon muchas tensiones en mí. Comencé a dar clases particulares durante dos años al tiempo que preparaba lo que podía las oposiciones, antes de empezar a trabajar como interino. Estas circunstancias hicieron que empezara a incrementarse el número de cigarrillos que fumaba al día, ya trabajando para la Consejería de Educación. Primero dos paquetes, luego tres y en la peor época como fumador había días que me fumaba hasta cinco paquetes de cigarrillos.

El último año antes de caer enfermo (por sexta vez) y recibir la pensión, me sentí muy bien trabajando, y solo fumaba un paquete y algo más. Luego he ido aumentando hasta tres paquetes diarios, situación en la que me he encontrado hasta hace una semana. Un amigo que también fuma me animó a ir a la unidad de tabaquismo del hospital Virgen Macarena, a la que hemos acudido, y nos han puesto un tratamiento. Estoy siguiéndolo, y espero que me ayude. Por ahora, con la medicación, voy reduciendo bastante el numero de cigarrillos que me fumo al día. El día 16 ya solo me fumaba 19 cigarrillos al día. Ruego a Dios por mi salud para que me ayude, sino a dejarlo definitivamente, que es lo que quiero, al menos a reducir la cantidad de tabaco que fumo diariamente. Mi esperanza mas profunda es dejarlo definitivamente y que con ello mi salud mejore. Yo llevo una odisea en la que el año que viene se cumplen 30 años fumando, y me digo cada día que ya va siendo hora de que lo deje. Estoy a ver si lo consigo. Esta es mi experiencia con el tabaco. Si podéis no fumar, no fuméis.

Jesús

UN DÍA DE MI VIDA

Vengo de la sesión de relajación y estoy en la mejor disposición para escribir este artículo. Un día de mi vida, de la vida de cualquier persona, puede parecer poco tiempo, pero no es así. Si compartimentamos el día en horas, minutos y segundos el tiempo se hace más largo y se le puede sacar más fruto. Es una visión más del tiempo relativo de Henri Bergson, al que ya le dediqué un artículo hace tiempo. Un día es mucho tiempo porque las veinticuatro horas se pueden alargar hasta un infinito relativo y exprimir el jugo hasta lo máximo.

Compartimentado el tiempo podemos sentir que disponemos de mucho más para vivir y poder afirmar con Roberto Benigni y Nicoleta Braschi que la vida es bella y lo es porque el tiempo es un tesoro maravilloso para vivir. El tiempo es la vida misma, el tiempo es, como decía San Agustín, un estado del alma. No hay presente ni pasado ni futuro. Los tiempos son estados del alma y no hay que diferenciarlos en absoluto.

Hay que mirar siempre hacia el presente, que es el estado del alma más inmediato que existe. En realidad lo que vivimos es un eterno presente. Hay que olvidarse del verso de Jorge Manrique, aquello de que cualquier tiempo pasado fue mejor. No hay que permitir que el tiempo nos tienda una trampa y nos engañemos a nosotros mismos pensando que todo lo vivido es siempre mejor que lo que vivimos en el presente. Y no es así. El tiempo presente nos permite tener la sensación de que estamos más vivos que nunca y que tenemos la verdad más absoluta de todas: que somos seres para la gloria presente de nuestras existencias.

Y es importante también a la hora de plantear este artículo el hecho de que tenemos que ser protagonistas de nuestras vidas, no como los personajes que interpretan Juan Diego y Juan Diego Botto en la película de Víctor García León “Vete de mí”, donde interpretan a dos personas sumamente inmaduras que no son protagonistas en absoluto de sus vidas sino que se dejan llevar por las circunstancias, como si todo su tiempo perteneciese a otros cuando en realidad no es así.

Yo por la mañana rezo a Dios. Le rezo oraciones tradicionales y otras infantiles aún, pero que todavía conservan su fascinación y su validez. Le doy gracias a Dios por darme otro día más para vivir y le pido que sea un día fructífero, rico lo máximo posible. Si no he tenido pesadillas ni malos sueños le doy las gracias por haber sido tan generoso conmigo porque se lo pido por las noches antes de dormir. Espero que el día nuevo tenga más sentido que nunca, que sea rico en todas sus facetas y que yo pueda sentirme orgulloso del uso de ese tiempo del que hablaba al principio del artículo. Pido a Dios que no malgaste mi tiempo porque es como malgastar la vida misma.

Al principio del día es cuando estoy peor con la ansiedad y el trastorno obsesivo compulsivo, que están íntimamente relacionados. De hecho ese trastorno es una variante de las muchas que tiene la ansiedad. Repaso física y mentalmente todas las cosas de la casa y todas las cosas que tengo que hacer durante el día o que hice el día anterior. Es una experiencia que me ocasiona un sufrimiento enorme y que me hace sentir el ser más desgraciado del mundo. De hecho llego a pensar que nadie está peor que yo. Es un sufrimiento espiritual y físico que no me deja tranquilo. Dura dos horas o más. Después, a lo largo del día, también repaso de vez en cuando, pero menos, las mismas cosas. Esta obsesión no me deja vivir. Me siento dependiente de ella totalmente y no sé cómo superarla. A veces intuyo un atisbo de esperanza que me hace sentir feliz aunque tenga el trastorno, pero no dura mucho tiempo. Es una felicidad perecedera, pero que merece la pena ser experimentada porque toda felicidad pequeña es grande. Aquí también se puede decir que la vida es bella porque uno tiene la voluntad de ser capaz de superar las adversidades y salir adelante con la fuerza necesaria para no caer en socavones aún más grandes.

Por la tarde es cuando suelo escribir. Actualmente estoy corrigiendo por primera vez el borrador de mi siguiente libro, que hace ya el número once de mi humilde carrera literaria. Se titula Pasión o espontaneidad y se trata de un largo poema fragmentado en 90 partes que intentan explicar la relación que existe ente el amor, la pasión y la muerte. El amor como sentimiento supremo que todo lo puede. La pasión como motor del amor mismo. Y la muerte como la parte negativa que puede poner punto y final tanto al amor como a la pasión, independientemente del orden. El libro está dedicado a una antigua amiga que precisamente se llamaba así, Pasión, de apellido Vázquez. La conocí en la Feria de Sevilla una noche y fue siempre una relación espontánea que nunca pasó de una sencilla amistad. Cuando nuestros caminos se separaron para siempre se me ocurrió la idea de escribir este libro con la palabra pasión en su título para jugar con la realidad de la pasión y el nombre de Pasión. Llevo mucho tiempo trabajando este libro, prácticamente desde que publiqué el último, Poemas que quise escribir. Suelo publicar un libro al año, lo cual me parece una buena media, la misma que la de Pedro Almodóvar, al que le gusta hacer una película cada año, exactamente igual que Woody Allen, quien siempre tiene una película nueva en cartelera cada año, actualmente A  Roma con amor.

Tengo muchas esperanzas puestas en este libro. Nunca hago una sola corrección, sino varias, antes de pasarlo a limpio en mi vieja máquina de escribir. El primer borrador lo escribo a mano, así como las correcciones, hasta que lo paso a limpio y luego empieza la rueda de la publicación, que suele durar sobre cuatro meses. Cuando llega el libro y lo cojo en mis manos es como tener la sensación de portar un niño en los brazos, algo nuevo que llega a la vida y que me da más vida aún.

Yo durante el día intento sacar esperanza de donde no la hay, por mal que me encuentre. Esa esperanza a veces dura unos breves minutos solamente, pero cuando llega la siento de verdad y me considero una persona feliz, en contraposición a la persona desgraciada que me siento cuando soy víctima del trastorno obsesivo compulsivo. Yo soy feliz con las cosas más pequeñas. No necesito grandes cosas para sentirme feliz. Me basta lo diminuto, lo aparentemente intrascendente. Pero basta con fragmentar el tiempo como decía al principio del artículo y entonces sentir unos segundos de felicidad tiene una riqueza enorme que se multiplica hasta el infinito aunque sólo dure un pequeño tracto de tiempo.

Por la noche suelo ver la tele, preferentemente programas deportivos o películas. Me encanta el cine y eso me ayuda después a llenar mis artículos de referencias cinematográficas. El cine es una fuente de enseñanza muy grande. El cine es vida. Siempre hay que decir como la canción: más cine por favor. No tengo preferencia por un género en concreto. Si la película es buena el género me es indiferente. Los miércoles voy al cine a ver una película de estreno. Este miércoles voy a ver Sin tregua, una película policíaca. Me apetece acción. Recientemente vi El profesor y El ladrón de palabras, dos películas estupendas y muy clarificadoras. La segunda tiene mucho que ver con la Literatura porque es la vida de tres escritores que se interrelacionan.

Tengo relación a diario con mis hermanas por teléfono. Me intereso por su estado de salud porque ambas están enfermas, sobre todo la pequeña que padece esclerosis múltiple. Lo está pasando muy mal y suele llorar conmigo y así se consuela, aunque a mí me afecta bastante por mi sensibilidad y porque yo tampoco me encuentro bien y también necesito a alguien con quien desahogarme. Pero bueno, lo hago como una acción de caridad cristiana y Dios me lo tendrá en cuenta.

Suelo tener una relación quincenal con mi hijo ya que estoy divorciado. Solemos ir a almorzar y charlamos de todas nuestras cosas. Me llevo bien con mi hijo, sobre todo teniendo en cuenta que tiene 22 años y es una edad especialmente difícil por los cambios hormonales y otras cuestiones. Tiene novia y está en quinto de carrera de Administración y Dirección de Empresas y Derecho, dos carreras en una. Él trabaja mucho. Se lo he intentado inculcar desde pequeño, igual que el hábito de la lectura. Siempre tiene un  libro pendiente de lectura. Igual que yo siempre tengo pendiente un libro de escritura.

Al final del día suelo hacer una reflexión ya en la cama de todo lo que he vivido y me ha ocurrido. Es una reflexión rápida, de apenas veinte minutos, para ver qué he hecho mal y qué puedo mejorar al día siguiente. Vuelvo a dialogar con Dios, pero sin rezar, una conversación directa como en mi libro Grito. Ese diálogo me sirve para pedirle al final descanso, consuelo y sueño y me suelo quedar dormido pronto.

Éste es más o menos mi día. Lo considero bastante rico aunque soy muy exigente conmigo mismo y quiero siempre más, pero menos de todo lo malo como mi trastorno. Espero que este artículo nos acerque aún más en este diálogo abierto que tenemos desde hace ya dos años más o menos. Que nuestra relación continúe es lo que deseo. Y que nunca nos falte, como suelo decir, la esperanza.

José Cuadrado Morales

LOS MALOS DIAS

A todas las mujeres nos desborda el hecho de ser madre pero más aún si tienes una enfermedad mental.

Esos malos días, por suerte los menos, en los que no te puedes levantar de la cama, lloras, gritas, te dan convulsiones, oyes voces, ves personas que nadie más ve. Eres incapaz de seguir con tu día a día y aún más de cuidar de tu hijo.

Gracias a dios tenemos a la familia que nos entienden y que siempre están a nuestro lado.

En mi caso en particular que no tengo pareja y vivo con mi madre y mi hermana son ellas mi punto de apoyo. Cuando he tenido algún ingreso le decían a mi hijo que me había ido a trabajar fuera, menos esta última vez que en agosto tuve mi último ingreso y le explicaron mi enfermedad a mi niño. Lo encajó bastante bien, ya había visto demasiadas caídas, demasiadas convulsiones.

Ahora ya no se enfada conmigo, todo lo contrario, se preocupa cuando me caigo, llama corriendo a mi madre si me ve convulsionar y le dice que me de la medicina, se acerca a mi cama y me pregunta si estoy mejor me besa y me dice cuánto me quiere. Y cuando me encuentro un pelín mejor me levanto y me siento en el salón para que no se preocupe tanto, quiero que me vea despierta aunque me sigan temblando las manos.

Se hace lo que sea para que tu hijo no se preocupe ni se sienta mal por culpa de un adulto.

 Inma.

LA CAMA ME COME

La cama me come cuando quiero levantarme y no puedo, me quedo sin fuerzas, es imposible y mira que me quiero levantar pero no puedo.

Si no fuera por mi madre que es la que me levanta, estaría todo el día dentro. Por la tarde después de comer quiero acostarme porque ya no puedo mas por mi enfermedad y se que me pongo peor, pero no lo puedo remediar, me voy a la cama. Ayer mismo  me puse a llorar  y me fui a la cama, se que tengo que cambiar el chip y salir mas porque lo que me da miedo es la calle ¡¡¡¡¡que tontería!!!!! con el sol tan bonito que hace .

Se que me tengo que aceptar,  sobre todo por mi hijo, que tengo que luchar mucho por él.  Muchas veces tengo muchas ganas de vivir y no meterme en una cama porque me estoy perdiendo la vida, pero otras, la cama me come. Ahora que son las navidades me voy a Madrid  donde viven mis hermanos y pienso pasármelo bien.

A si es que voy a dejar la cama y vivir más, pienso darme unos buenos paseos por el pueblo. Tengo que aceptar que la cama es para la noche y no para el día.

Isabel

LOS VIEJOS ROCKEROS NUNCA MUEREN

El 25 de noviembre en Londres tuvo lugar el primero de una serie de conciertos con los que los Rolling Stones celebran el cincuenta aniversario de su creación. Según las propias palabras de Keith Richards la banda aún no está preparada para salir a la carretera de hecho, comenta que vé mas realista salir de gira en 2013.

 Rolling Stones es una banda británica originaria de Londres. Desde su gira por los Estados Unidos en 1969 se autodenominaron la banda de rock and roll más grande del mundo. La banda se fundó en abril de 1962.A mí me produce mucha admiración por sus componentes y por su música. Es una banda con mucha experiencia y tiene una discografía muy grande con muchos discos en estudio y conciertos por todo el mundo. La calidad de sus componentes ha sido siempre impresionante, con mucho publico en sus conciertos. Los Rolling Stones han tenido muchos componentes a lo largo de su época musical. Es increíble que en los tiempos que estamos todavía están ahí, al pié del cañón. Continúan dando mucha guerra en  los conciertos y en los discos que todavía siguen sacando, con mucho publico en todos lados. Siempre han tenido muchos géneros en su música: Rock, Rock and Roll, Blues, Hard Rock, R&B, y Rock Psicodélico. 

A mí personalmente los Rolling me gustan mucho, porque cantan muy bien y su sonido es fantástico y muy bueno. No decepcionan, se ganan a pulso su publico y sus discos. Es una banda veterana con muchos años de historia. La edad y el año de nacimiento de los miembros de los Rolling Stones es la siguiente, Mick Jagger (Michael Philip Jagger); 69 años(26 de julio de 1943), Keith Richards; 68 años (18 de diciembre de 1943), Charlie Watts-; 71 años ( 2 de junio de 1941), y Ron Word; 65 años (1 de junio de 1947). Mucha gente a su edad pasa los días jugando al dominó en el “hogar del pensionista” y ellos con casi setenta años otra vez en la carretera. Aquí se confirma el dicho de que "los viejos rockeros nunca mueren"

Genaro

ESTIMULA TU MENTE

Ejercicios de estimulación cognitiva. Busca diez diferencias entre esta imagen y su especular.

UN DÍA ESPECTACULAR

Hoy hace un día espectacular, me he levantado, he salido de casa y en la carretera había escarchada y se respiraba un ambiente fresco y natural. El invierno me gusta, es espectacular. Hoy si puedo iré a correr por la sierra y me divertiré oliendo el tomillo y la hierba  fresca del campo, esto me ayuda a evitar los pensamientos negativos y extraños como yo digo “los malos espíritus de mi cabeza” y desconectar abriendo un nuevo día de lucha contra la enfermedad. Soy una persona sana y me gusta mucho el deporte algunos me dirán “el loco del deporte” porque casi siempre estoy hablando de lo mismo, si pudiera y tuviera dinero me haría una piscina y una pista de atletismo para mi solo para llevarme todo el día entrenando. Me gustaría enseñar e instruir a niños sobre yoga y deporte,  para que supieran lo que es la vida sana y quitarlos de este mundo de injusticias.

Juanan

DESEOS

Os deseamos una navidad llena de todo lo mejor y un año Nuevo repleto de todo lo que se parezca a vuestras ilusiones.

RELATO

DESCALZO

El humo del cigarrillo me estaba entrando en los ojos, así que decidí fumármelo antes de volver a levantar la trampilla del contenedor para coger los cartones. Por suerte esa noche el contenedor estaba lleno, así que seguro que encontraría uno lo suficientemente largo como para poder hacerme una cama cómoda. Ayer no tuve tanta suerte y donde dormí, en la Encarnación, acababa de pasar el camión de la basura y se los habían llevado. Es raro, por la noche no retiran los contenedores del centro  hasta después de media noche pero seguro que estarán haciendo obras por algún lado y tiene que retirarlos antes de que sea demasiado tarde.

Cogí un cartón de una caja de un televisor grande. Lo suficiente para poder estirar los pies sin que estos me queden fuera. Dormir sin zapatos es un riesgo que hay que corre, por la noche puede venir alguien y robártelos y al día siguiente te quedas sin ellos y, te jodes y punto, pero después de estar todo el día andando de un lado para otro y sin descansar bien, cuando llega la noche los pies te piden un poco de alivio y respiro y te lo agradecen. Una vez en Ponce de León, durmiendo entre los aparcamientos de los coches y los pequeños jardines, teníamos los zapatos quitados un compañero y yo. A mí me quitaron una manta que no utilizaba pero a mi  compañero le quitaron los zapatos. Menos mal que nos encontramos a otro que estaba también viviendo en la calle y tenía unos zapatos de sobra y nos los dio.

Ya tengo los cartones suficientes. Con todos estos puedo pasar esta noche de una forma cómoda. No solo voy a dormir sobre cartones, en mi macuto, amigo inseparable que llevo todo el día a cuestas y que no dejo en ningún sitio, tengo una manta y una colchoneta de las que se usan para los sacos de dormir. Los cartones son para aislarme del frío y sucio suelo. Aunque tengo que decir que si, por razones superiores a mí, he perdido el saco, la manta o la colchoneta y he tenido que dormir tan solo sobre los cartones, también lo he hecho, aunque eso si, en verano y aquí en Sevilla, que el clima es suave.

Ahora en invierno es diferente, se te hielan los pies y las manos.  Las orejas no las sientes, aunque estoy contento porque  hoy es navidad y en el albergue me han regalado un gorro de Papá Noel y esta noche dormiré con la cabeza caliente.

La pluma negra.

ESPACIO POÉTICO

MELODÍA POÉTICA.

¡¡¡La dulce balada del recorrido del canto del viejo escribir

qué toca la luna.

Melodía poética de mis sueños surrealistas

del corazón del recuerdo del viejo tiempo.

La enmudecida noche en el camino y el viejo pueblo

con el aliento del canto de la libertad del alma

en la hora poética de la melodía juglar.

De mis pensamientos perdidos del instinto vivido

la entusiasta poética ilusión del escribir

de la vivencia de las palabras de la NAVIDAD qué nunca perdí...!!!

Miguel Antonio Moreno Martín

http://poesiamarchena.wordpress.com/

HACIENDO DEPORTE

A mi me gusta hacer deporte, al aire libre, o en el gimnasio, pero me gusta mas el gimnasio, porque se esta en compañía de la monitora, que te anima, estas con mas gente, y es mas divertido porque escuchas música, yo las clases que he probado son: Pilates, que se trabaja con el cuerpo y la respiración, el spinning ,que es la bici sirve para quemar la grasa, es mas pesado que las otras clases, y también el body pump, que se practica con las pesas, y con las mancuernas, se hacen varios movimientos con el cuerpo.

 A mi lo que mejor se me da es el spinning, y el body pump, y de la planta de abajo, porque el gimnasio tiene dos alturas, me gusta un poco de todo, las maquinas de pesas para los brazos y las piernas, la cinta de andar, la bici elíptica, y el banco de hacer abdominales. 

Hace tiempo que no voy, pero estoy deseando que llegue enero para apuntarme otra vez, pero  estoy temiendo a las agujetas, el deporte es genial porque hace que te sientas bien, con mas ánimo y además te sientes mas relajada.

Ludi.

GUISO DE CARRILLADA; DE LUJO

INGREDIENTES

• Carrillada 2 kg.
• Cebollas grandes 2
• Zanahorias 2
• 6 dientes de ajos
• Pimiento choricero 
• 1 cuchara sopera
• Wisky
• 1 botella tinto(cosecha - no crianza)
• Sal, pimienta, tomillo
• 3 hojas de laurel

PREPARACIÓN

Se refríe la carne en un poco de aceite solo con sal y pimienta, cuando este dorada, apartarla. En la misma olla se hace el sofrito por este orden; el ajo laminado, la cebolla a trozos y la zanahoria. Cuando esté listo se le echa la carne, se le añade el laurel y el tomillo y se le pone un vasito de whisky, se da vueltas hasta mezclarlo todo muy bien y se le añade la botella de tinto entera. Se deja hervir unos minutos, antes de tapar la olla Express hay que asegurarse de que la carne  está cubierta, si hace falta se añade un poco de agua.

Se tapa la olla y se deja una hora hirviendo mas o menos cuando la carne este tierna se retira y se tritura toda la salsa con la batidora y de nuevo de le añade la carne. * Si se quiere se le puede poner una onza de chocolate negro puro

¡Listo para comer!

DIABETES UNA ENFERMEDAD DIFÍCIL DE LLEVAR

Hola que tal a todos, hoy voy a escribiros de  la diabetes y el día a día de las personas que padecen esta enfermedad, yo la tengo y la verdad es muy incomoda, todos los días me tengo que poner insulina y los perfiles tres días a la semana. En fin un incordio pero hay que hacerlo porque sino me cuido esta enfermedad puede atacar a ojos, a la circulación  y demás cosas que son muy desagradables. La diabetes se puede llevar bien con buenas dietas y haciendo deporte o andando, todo depende de la edad del enfermo. Yo practico mucho deporte para estabilizar el nivel de azúcar en sangre, que mas puedo deciros, lo de antes, hacer ejercicio y llevar una vida saludable y lógicamente no pasarse sobre todo estas navidades de los dulces y mantecados ,vamos lo típico de la navidad. Yo os aconsejo que seáis cautos, yo lo soy, y tan solo es cuestión de mentalizarse y de acostumbrarse, yo lo hago y funciona.  Cuesta mucho trabajo decir no a los dulces pero no hay otra opción porque la salud es lo mas importante, sin salud nos limitamos en muchos sentidos y hay que echarle valor a la vida y llevar una vida normal con la diabetes o sin ella. Este es el consejo de un diabético, pues nada ya os dejo y nada que paséis una buena navidad y un prospero año nuevo hasta otra.

David

ESTIMULA TU MENTE

Estimulación cognitiva. Hay un refrán que dice "la cara es el espejo del alma". Empareja, en función de la expresión facial, cada cara con el pensamiento que mas se le aproxime.

Soluciones ejercicios anteriores:

SABÍAS QUÉ...

Hasta hace poco creía que los únicos sabores básicos que existían eran el dulce, el salado,  el amargo y  ácido, pero resulta que existe otro sabor que es desconocido para casi todo el mundo que es el umami.

Umami significa sabor gustoso, proviene del idioma japonés y significa sabor agradable gustoso. Esta palabra fue elegida por  su descubridor el profesor kikunae kedor en 1908.

Umami representa el sabor del aminoácido, aunque puede descubrirse como un agradable sabor cárnico a caldo que deja una sensación prolongada que hace agua a la boca y que cubre toda la lengua.Y se encuentra  en muchos alimentos que podemos consumir a diario como por ejemplo los pescados. carnes,  mariscos y verduras.  

Entre las verduras se encuentran los champiñones, tomates, col china, espinacas

o té verde y la leche materna: Todas las papilas gustativas de la lengua pueden detectar el sabor umami.

En  francés, inglés, español  la palabra umami significa lo mismo.

J.G

FRACTALES

Para acercarnos un poco a los fractales habría que decir de donde viene el nombre de fractal: viene de objetos o entes geométricos, espacios geométricos, que pueden tener una dimensión que sea una parte (o fracción para entendernos) de las habituales. Estamos acostumbrados a los espacios geométricos habituales: la recta, de dimensión 1, el plano, de dimensión 2 y el espacio, de dimensión 3. Pues pueden darse espacios geométricos que tengan por ejemplo dimensión ½.

El conjunto de puntos que se obtiene al dividir un segmento en cuatro partes y quedarse con dos (por ejemplo las de los extremos), repitiendo este proceso con cada una de las partes con que nos vamos quedando, hasta el infinito, tiene dimensión ½:

Tratando análogamente un segmento a como se ha hecho con el anterior, pero dividiéndolo en tres partes y quedándonos con dos, y repitiendo el proceso hasta el infinito con los segmentos que van quedando, se obtiene un conjunto de puntos al que se llama conjunto de Cantor, y que tiene dimensión log2/log3, aproximadamente 0,63.

Estas dimensines se denominan dimensiones fractales de Hausdorff, pues fue este matemático el que aportó un método para determinarlas.

A los conjuntos anteriores se les llama autosemejantes, y son entes u objetos geométricos cuya estructura se repite, en gran medida, a diferentes escalas, hasta el infinito. Sirven para modelar muchos aspectos de la realidad.

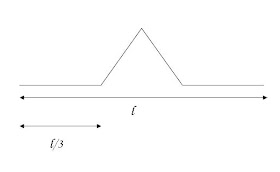
Un fractal muy interesante es el conocido como la curva de Koch. Es una figura que se repite a si misma infinitas veces a diferentes escalas. Se obtiene dividiendo un segmento en tres partes, quedándose con los extremos y construyendo sobre la que hemos eliminado dos lados de un triángulo equilátero (en el centro) que midan la tercera parte del segmento. Se repite este proceso con cada una de las partes que se van obteniendo, hasta el infinito. El fractal que se obtiene tiene dimensión log4/log3, aproximadamente 1,26.

La medida ordinaria de fractales como los anteriores es nula o infinita. Sin embargo la medida de los fractales hay que hacerla en su dimensión. Medidos en su dimensión estos fractales de que hablamos tienen medida finita no nula.

Tomemos el segmento unidad para realizar los cálculos.

La medida ordinaria del conjunto de dimensión ½ sería nula ya que contando el conjunto :

2ⁿ .(1/4ⁿ ) = 1/2ⁿ   que tiende a cero cuando n tiende a infinito

Si tenemos en cuenta que el conjunto tiene dimensión fractal ½ se tendría que la medida del conjunto sería:

2ⁿ .(1/4ⁿ )^1/2 = 1ⁿ =1

Igual ocurre con la curva de Koch:
Tomando el segmento unidad, la medida ordinaria de este conjunto conduce a:

4ⁿ .(1/3ⁿ ) = (4/3)ⁿ  que tiende a infinito cuando n tiende a infinito             

Si llamamos s a la dimensión de este conjunto se tiene que:

4ⁿ .(1/3ⁿ )^s =1ⁿ = 1 si s = log4/log3

Este fractal sirve para modelar aspectos físicos de la realidad, como las fronteras. Por ejemplo, la costa de Gran Bretaña se ha estimado empíricamente como un fractal de dimensión 1,3 muy parecida a la dimensión de la curva de Koch. Todavía la frontera entre España y Portugal lleva a una dimensión más cercana a la de esta curva. La costa de Noruega, un poco mas complicada que la de Gran Bretaña , lleva a un fractal de dimensión 1,5.

Otro fractal interesante es el conocido como curva de Hilbert. Se obtiene a partir de un cuadrado: se divide éste en cuatro cuadrados y los centros de los cuadrados se unen mediante una poligonal. Luego cada cuadrado se divide en otros cuatro y se vuelven a unir los centros mediante otra poligonal. Se repite este proceso hasta el infinito. El resultado es la curva de Hilbert. Esta curva recubre completamente el cuadrado. Es un fractal de dimensión 2.

Con esta curva, tomando segmentos unidad, se obtiene llamando s a la dimensión del objeto, la medida:

(4ⁿ -1).(1/2ⁿ )^s que cuando n tiende a infinito tiende a  4ⁿ .(1/2ⁿ )^s

       y      4ⁿ .(1/2ⁿ )^s = 1ⁿ =1  si s = 2                   

Este fractal sirve para modelar aspectos físicos de la realidad, lo que se llaman árboles. Entre estos podemos encontrar por ejemplo un río o la red arterial de una persona. Un rio, junto con sus afluentes, arroyos, y todas las confluencias de agua que se dan en el mismo puede ser modelado mediante un fractal parecido a la curva de Hilbert. Con la red de arterias ocurre algo parecido.

A propósito de dimensiones las que conocemos habitualmente son las tres espaciales y la que podemos considerar la temporal, la última se puede apreciar en el cine 4D que hay en Isla Mágica. 4D significa precisamente esto, en cuatro dimensiones. Para hacernos una idea de en lo que quiere significarse la proyección que se hace en este cine, podéis fijaros en el siguiente esquema, donde t significa tiempo:

La proyección va sumergiéndonos en las tres dimensiones espaciales y en la temporal, pudiendo apreciarlas conjuntamente, y por separado si nos fijamos en cada una de ellas individualmente.

Nota:

Para ver con claridad cual es la dimensión fractal de un cuadrado pensemos en como recubrirlo completamente. El proceso consiste en ir dividiendo el cuadrado en otros cuadrados: primero en cuatro cuadrados, e ir uniendo sus centros mediante una poligonal sencilla cuadrada, luego dividimos el cuadrado original en dieciséis cuadrados, y unimos los centros mediante dos poligonales sencillas cuadradas, y así sucesivamente, hasta el infinito.

Se tiene entonces que contando, si llamamos s a la dimensión del cuadrado se tendría:

  4ⁿ .(1/2ⁿ )^s = 1ⁿ =1    si   s = 2

Ejemplos de fractales en la naturaleza:

Jesús Ocaña